Decision Tree makes the choice of the best attribute within the current attribute sets directly. Here I will present detailedly my python code of the Decision tree algorithm.
INformation entropy
Information entropy is a widely used measure of the set purity of sample. If there are N samples belonging to d categories in set D, let \(p_k=N_k/N\) stands for the probability of selecting a k sample randomly, them we have:
\[Ent\left ( D \right )=-\sum_{k=1}^{d}p_k\log_{2}^{p_k}\]Assume there are V underlying values of one discrete attribute a, if we divide sample D in accordance with property a, then V branches will be created, and we denote the sample amount in branch v as \(N_v\), then we are able to calculate the information entropy of all branches, we wed it together with there weights in total sample, get the definition of information entropy below:
\[Gain\left ( D,a \right )=Ent\left ( D \right )-\sum_{v=1}^{V}\frac{N_v}{N}Ent\left ( D_v \right )\]Usually higher information entropy represents better purity of our sample based on attribute a.
Gain ratio
According to materials I found, the largest \(Gain\left ( D,a \right )\) does not always match the best attribution as it lacks of the generalization ability. Now I will introduce “gain ratio” to you guys.
\[GainRatio\left ( D,a \right )=\frac{Gain\left ( D,a \right )}{IV\left ( a \right )}\] \[IV\left ( a \right )=-\sum_{v=1}^{V}\frac{N_v}{N}\log_{2}^{\frac{N_v}{N}}\]We choose property with the highest gain ratio as our best attribute. \(IV\left ( a \right )\) is the nature property of attribut a. As far as I know, this gain ratio may perfer attribute which target sample amount is releatively lower, thus I need to calculate gain ratios for all attributes, drop half which gain ratios are below the average level.
Gini index
other method for constructing our decision tree is Gini index. If we select two indiciduals from a large sample, the probability that they belong to different categories is called Gini.
\[Gini\left ( D \right )=1-\sum_{v=1}^{d}p_v^2\]It’s direct that smaller Gini means purer dataset. It can be used to select attributes after acquire Gini Index:
\[GiniIndex\left ( D,a \right )=\sum_{v=1}^{V}\frac{N_v}{N}Gini\left ( D_v \right )\]We choose the attribute with the lowest Gini Index as our target, and we get what is called as CART decision tree.
Now I will show you very detailedly about how to construct your own Decision Tree with Python code step by step.
from sklearn.datasets import load_iris
import numpy as np
import math
from collections import Counter
class decisionnode:
def __init__(self, d=None, thre=None, results=None, NH=None, lb=None, rb=None, max_label=None):
self.d = d # d表示维度
self.thre = thre # thre表示二分时的比较值,将样本集分为2类
self.results = results # 最后的叶节点代表的类别
self.NH = NH # 存储各节点的样本量与经验熵的乘积,便于剪枝时使用
self.lb = lb # desision node,对应于样本在d维的数据小于thre时,树上相对于当前节点的子树上的节点
self.rb = rb # desision node,对应于样本在d维的数据大于thre时,树上相对于当前节点的子树上的节点
self.max_label = max_label # 记录当前节点包含的label中同类最多的label
It is straight that the first procedure is loading our target dataset and finish the basic DecisionTree settings.
def entropy(y):
'''
计算信息熵,y为labels
'''
if y.size > 1:
category = list(set(y))
else:
category = [y.item()]
y = [y.item()]
ent = 0
for label in category:
p = len([label_ for label_ in y if label_ == label]) / len(y)
ent += -p * math.log(p, 2)
return ent
def Gini(y):
'''
计算基尼指数,y为labels
'''
category = list(set(y))
gini = 1
for label in category:
p = len([label_ for label_ in y if label_ == label]) / len(y)
gini += -p * p
return gini
The code above is about calculating three relevent values introdued already.
def GainEnt_max(X, y, d):
'''
计算选择属性attr的最大信息增益,X为样本集,y为label,d为一个维度,type为int
'''
ent_X = entropy(y)
X_attr = X[:, d]
X_attr = list(set(X_attr))
X_attr = sorted(X_attr)
Gain = 0
thre = 0
for i in range(len(X_attr) - 1):
thre_temp = (X_attr[i] + X_attr[i + 1]) / 2
y_small_index = [i_arg for i_arg in range(
len(X[:, d])) if X[i_arg, d] <= thre_temp]
y_big_index = [i_arg for i_arg in range(
len(X[:, d])) if X[i_arg, d] > thre_temp]
y_small = y[y_small_index]
y_big = y[y_big_index]
Gain_temp = ent_X - (len(y_small) / len(y)) * \
entropy(y_small) - (len(y_big) / len(y)) * entropy(y_big)
'''
intrinsic_value = -(len(y_small) / len(y)) * math.log(len(y_small) /
len(y), 2) - (len(y_big) / len(y)) * math.log(len(y_big) / len(y), 2)
Gain_temp = Gain_temp / intrinsic_value
'''
# print(Gain_temp)
if Gain < Gain_temp:
Gain = Gain_temp
thre = thre_temp
return Gain, thre
def Gini_index_min(X, y, d):
'''
计算选择属性attr的最小基尼指数,X为样本集,y为label,d为一个维度,type为int
'''
X = X.reshape(-1, len(X.T))
X_attr = X[:, d]
X_attr = list(set(X_attr))
X_attr = sorted(X_attr)
Gini_index = 1
thre = 0
for i in range(len(X_attr) - 1):
thre_temp = (X_attr[i] + X_attr[i + 1]) / 2
y_small_index = [i_arg for i_arg in range(
len(X[:, d])) if X[i_arg, d] <= thre_temp]
y_big_index = [i_arg for i_arg in range(
len(X[:, d])) if X[i_arg, d] > thre_temp]
y_small = y[y_small_index]
y_big = y[y_big_index]
Gini_index_temp = (len(y_small) / len(y)) * \
Gini(y_small) + (len(y_big) / len(y)) * Gini(y_big)
if Gini_index > Gini_index_temp:
Gini_index = Gini_index_temp
thre = thre_temp
return Gini_index, thre
The third step is about calculating the wanted attribute with largest gain ratio or smallest Gini index.
def attribute_based_on_GainEnt(X, y):
'''
基于信息增益选择最优属性,X为样本集,y为label
'''
D = np.arange(len(X[0]))
Gain_max = 0
thre_ = 0
d_ = 0
for d in D:
Gain, thre = GainEnt_max(X, y, d)
if Gain_max < Gain:
Gain_max = Gain
thre_ = thre
d_ = d # 维度标号
return Gain_max, thre_, d_
def attribute_based_on_Giniindex(X, y):
'''
基于信息增益选择最优属性,X为样本集,y为label
'''
D = np.arange(len(X.T))
Gini_Index_Min = 1
thre_ = 0
d_ = 0
for d in D:
Gini_index, thre = Gini_index_min(X, y, d)
if Gini_Index_Min > Gini_index:
Gini_Index_Min = Gini_index
thre_ = thre
d_ = d # 维度标号
return Gini_Index_Min, thre_, d_
This is for confirming the best attribute.
def devide_group(X, y, thre, d):
'''
按照维度d下阈值为thre分为两类并返回
'''
X_in_d = X[:, d]
x_small_index = [i_arg for i_arg in range(
len(X[:, d])) if X[i_arg, d] <= thre]
x_big_index = [i_arg for i_arg in range(
len(X[:, d])) if X[i_arg, d] > thre]
X_small = X[x_small_index]
y_small = y[x_small_index]
X_big = X[x_big_index]
y_big = y[x_big_index]
return X_small, y_small, X_big, y_big
def NtHt(y):
'''
计算经验熵与样本数的乘积,用来剪枝,y为labels
'''
ent = entropy(y)
print('ent={},y_len={},all={}'.format(ent, len(y), ent * len(y)))
return ent * len(y)
def maxlabel(y):
label_ = Counter(y).most_common(1)
return label_[0][0]
I have to say this part is derived from materials since I have not learnt about the strategy of purning. The function has been illustrated in Chinese in the annotation.
def buildtree(X, y, method='Gini'):
'''
递归的方式构建决策树
'''
if y.size > 1:
if method == 'Gini':
Gain_max, thre, d = attribute_based_on_Giniindex(X, y)
elif method == 'GainEnt':
Gain_max, thre, d = attribute_based_on_GainEnt(X, y)
if (Gain_max > 0 and method == 'GainEnt') or (Gain_max >= 0 and len(list(set(y))) > 1 and method == 'Gini'):
X_small, y_small, X_big, y_big = devide_group(X, y, thre, d)
left_branch = buildtree(X_small, y_small, method=method)
right_branch = buildtree(X_big, y_big, method=method)
nh = NtHt(y)
max_label = maxlabel(y)
return decisionnode(d=d, thre=thre, NH=nh, lb=left_branch, rb=right_branch, max_label=max_label)
else:
nh = NtHt(y)
max_label = maxlabel(y)
return decisionnode(results=y[0], NH=nh, max_label=max_label)
else:
nh = NtHt(y)
max_label = maxlabel(y)
return decisionnode(results=y.item(), NH=nh, max_label=max_label)
def printtree(tree, indent='-', dict_tree={}, direct='L'):
# 是否是叶节点
if tree.results != None:
print(tree.results)
dict_tree = {direct: str(tree.results)}
else:
# 打印判断条件
print(str(tree.d) + ":" + str(tree.thre) + "? ")
# 打印分支
print(indent + "L->",)
a = printtree(tree.lb, indent=indent + "-", direct='L')
aa = a.copy()
print(indent + "R->",)
b = printtree(tree.rb, indent=indent + "-", direct='R')
bb = b.copy()
aa.update(bb)
stri = str(tree.d) + ":" + str(tree.thre) + "?"
if indent != '-':
dict_tree = {direct: {stri: aa}}
else:
dict_tree = {stri: aa}
return dict_tree
def classify(observation, tree):
if tree.results != None:
return tree.results
else:
v = observation[tree.d]
branch = None
if v > tree.thre:
branch = tree.rb
else:
branch = tree.lb
return classify(observation, branch)
def pruning(tree, alpha=0.1):
if tree.lb.results == None:
pruning(tree.lb, alpha)
if tree.rb.results == None:
pruning(tree.rb, alpha)
if tree.lb.results != None and tree.rb.results != None:
before_pruning = tree.lb.NH + tree.rb.NH + 2 * alpha
after_pruning = tree.NH + alpha
print('before_pruning={},after_pruning={}'.format(
before_pruning, after_pruning))
if after_pruning <= before_pruning:
print('pruning--{}:{}?'.format(tree.d, tree.thre))
tree.lb, tree.rb = None, None
tree.results = tree.max_label
if __name__ == '__main__':
iris = load_iris()
X = iris.data
y = iris.target
permutation = np.random.permutation(X.shape[0])
shuffled_dataset = X[permutation, :]
shuffled_labels = y[permutation]
train_data = shuffled_dataset[:100, :]
train_label = shuffled_labels[:100]
test_data = shuffled_dataset[100:150, :]
test_label = shuffled_labels[100:150]
tree1 = buildtree(train_data, train_label, method='Gini')
print('=============================')
tree2 = buildtree(train_data, train_label, method='GainEnt')
a = printtree(tree=tree1)
b = printtree(tree=tree2)
true_count = 0
for i in range(len(test_label)):
predict = classify(test_data[i], tree1)
if predict == test_label[i]:
true_count += 1
print("CARTTree:{}".format(true_count))
true_count = 0
for i in range(len(test_label)):
predict = classify(test_data[i], tree2)
if predict == test_label[i]:
true_count += 1
print("C3Tree:{}".format(true_count))
#print(attribute_based_on_Giniindex(X[49:51, :], y[49:51]))
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
import treePlotter
import matplotlib.pyplot as plt
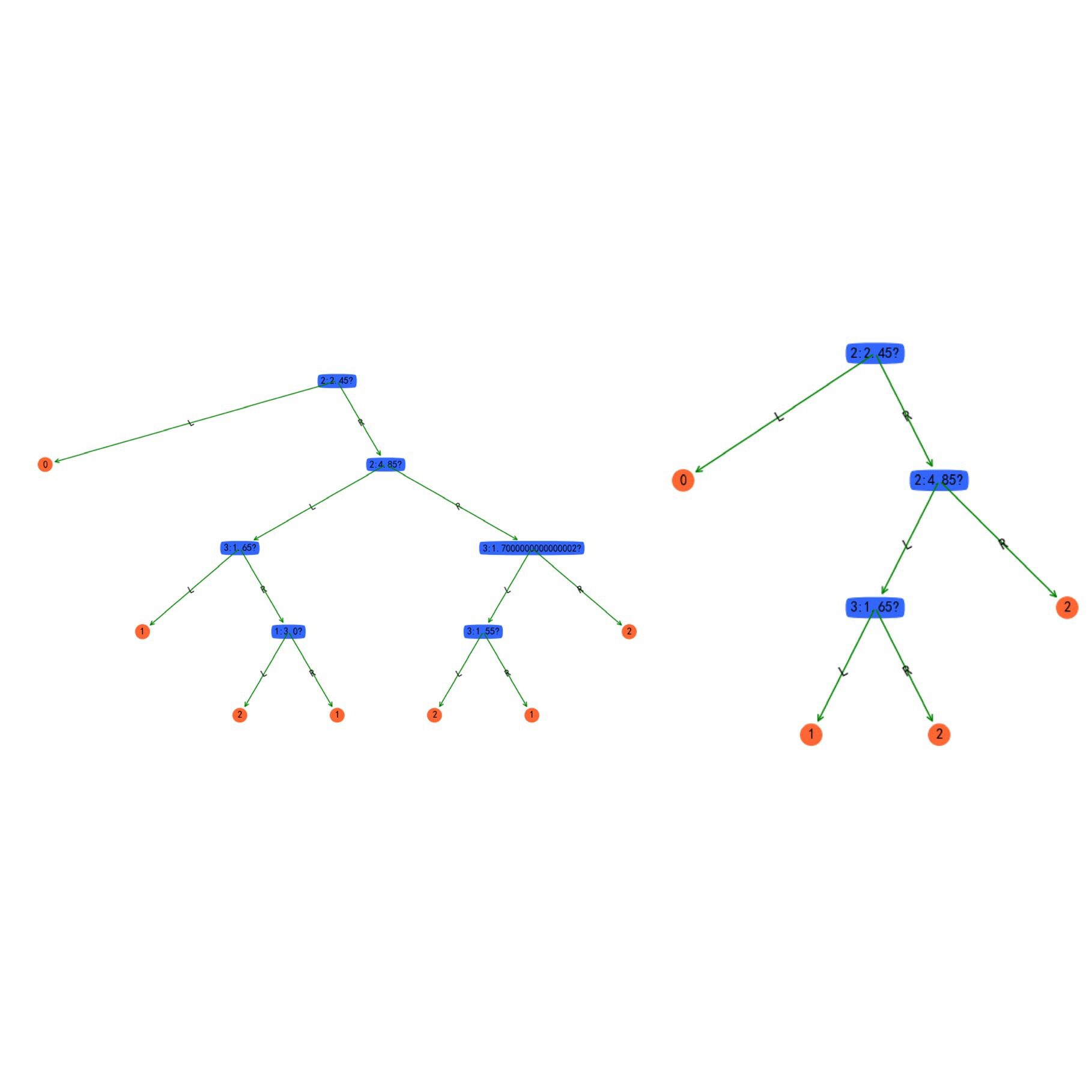
treePlotter.createPlot(a, 1)
treePlotter.createPlot(b, 2)
# 剪枝处理
pruning(tree=tree1, alpha=4)
pruning(tree=tree2, alpha=4)
a = printtree(tree=tree1)
b = printtree(tree=tree2)
true_count = 0
for i in range(len(test_label)):
predict = classify(test_data[i], tree1)
if predict == test_label[i]:
true_count += 1
print("CARTTree:{}".format(true_count))
true_count = 0
for i in range(len(test_label)):
predict = classify(test_data[i], tree2)
if predict == test_label[i]:
true_count += 1
print("C3Tree:{}".format(true_count))
treePlotter.createPlot(a, 3)
treePlotter.createPlot(b, 4)
plt.show()
The final part is about constructing our DecisionTree through iterations. Both of them produces a satisfying result with 0.96 accuracy, the figures below shows the outcome before and after purning.