Microeconometrics

KL DIVERGENCE EXPALNATIONS

Microeconometrics

Posted by ELVIS on March 29, 2019

Hey

这是我的第一篇博客。

HW1 Youwen Zhang

In this file I will be glad to talk about how does the KL Divergence functions and why its not a proper distance measure. Several detailed mathematical functions will be provided as proof.

What’s the definition of KL divergence and what’s the function?

In mathematical statistics, the Kullback–Leibler divergence (also called relative entropy) is a measure of how one probability distribution is different from a second, reference probability distribution. ( wikipedia kL-Divergence ) In my opinion, KL Divergence is a measure of how much information loss we have created when we use one distribution to approximate another.

It’s obviously that we are looking forward to build a model which is as basic and simple as possible to describe our sample, or in”machine-learning” words we do the dimensionality reduction and we’d like to preserve as much information of the original input as possible. But the question is that can we get close to the true situation as we simplify our assumptions, can we do both? The KL Divergence is such a tool that is interpreted as loss function.

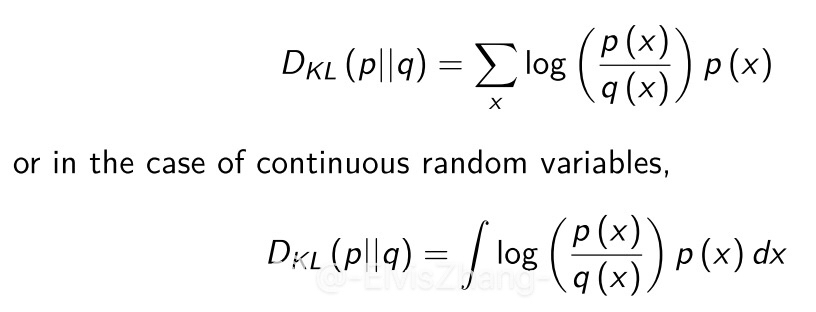
KL Divergence

And here I just list my python code about how it is calculated. I will be honered if you can help to test and improve my code.

import numpy as np
import scipy.stats

 #Generate two discrete random variables x and y
x = [np.random.randint(1, 10) for i in range(9)]
print(x)
print(np.sum(x))
px = x / np.sum(x)
print(px)
y = [np.random.randint(1, 10) for i in range(9)]
print(y)
print(np.sum(y))
py = y / np.sum(y)
print(py)

KL = scipy.stats.entropy(x, y)
print(KL)

Why is KL Divergence not a distance measure?

To be available to measure distance, three elements must be satisfied: non-negativity, triangle inequality, as well as symmetry.

  • Non-negativity

    Proof of Non-negativity by using Jensen Inequality, which is pretty natural.

  • Asymmetry

    Let’s introduce a pretty straightforward example instead of worms’ teeth. Here are three distributions: A(100) = 1/2, A(99) = 1/2 B(100) = 1/3, B(99) = 2/3 C(100) = 1/4, C(99) = 3/4 Calculate KL-Divergence we get D(A||B) = 1/2log(3/2) + 1/2log(3/4) = 1/2log(9/8) D(B||A) = 1/3log(2/3) + 2/3log(4/3) = 1/3log(32/27) Since D(A||B) != D(B||A), this measure is asymmetry.

  • Triangle Inequality not fitted
    D(B   C) = 1/3log(4/3) + 2/3log(8/9) = 1/3log(256/243)        
    D(A   C) = 1/2log(2) + 1/2log(2/3) = 1/2log(4/3)        
    Since D(A   C) - (D(A   B) + D(B   C)) = 1/6log(3/2) > 0, the triangle inequality doesn’t fit.
Thus the KL-Divergence is definitely not a distance measure. This asymmetry, however, can be exploited in the sense that in cases where we wish to learn the parameters of a distribution q that over-compensates for p, we can minimize KL(p   q). Conversely when we wish to seek just the main components of p with q distribution, we can minimize KL(q   p). As we have seen, the KL Divergence allows us to learn very complex approximation of our sample data, and If you are thirsty for more detailed explanations, you can go search for relative resources like AM207 and other professional books.
CATALOG
    FRIENDS